[कमेन्टहरुका आधारमा मैले यो ब्लगमा शंकालुहरुका लागि भित्र थप अपडेट गरेको छु]

अर्ध-ज्ञान प्रयोग गरेर कुनै पनि बिषयको गलत ब्याख्या गर्नु भनेको ४=५ प्रमाणित गर्नु जस्तै हो । गलत आधार लिएर गरेका दावी पनि अचम्मका हुन्छन्, दावीका स्तर क्रान्तिकारी हुँदै जान्छन् । यस्ता पुष्टि नै नभएका बिज्ञानका समाचार बेला बखत आइरहन्छन -त्यो पनि नाम चलेका पत्रिकाहरुमा | सरकारले अन्तर्राष्ट्रिय चिनारीमा पहल गरिदिएन भनेर गाली पनि गरिन्छ । आउनुहोस् पहिला स्कुलतिर सिकेको ४ = ५ प्रमाणित गरौँ ।
यो त पक्कै पत्याउने कुरा भएन (गल्ति एउटा स्टेपमा मात्र छ, आफै फेला पार्नुस) । तर यो प्रमाणलाइ मान्ने हो भने ५ लाख ऋण तिर्नु भए ४ लाख तिरे भयो या दुवै साइडमा जोड्ने या गुणन गरेर जति बराबर जति पनि निकाल्न सकिएला ।

अब प्रसंग जोड्न खोजेको कुरा तिर जाउँ । करिब ४-५ वर्ष अघि एउटा नेपाली दैनिकको मुखपृष्ठमा “नेपालमा नयाँ आर्किमिडिज” या यस्तै सारको एउटा ठुलो समाचार आयो । स्वाभाविक रुपले कुनै नेपालीले बिज्ञानको क्षेत्रमा ठुलै काम गरेछ भनेर निकै खुशी लाग्यो, र चाख मानेर पढ्न बसें । लेखिएको थियो “२२०० वर्ष पुरानो आर्किमिडिजको सिद्धान्त गलत साबित” । केहि लाइन पढेपछि मेरो आशा खरानी भयो र खुशीले ठ्याक्कै १८० डिग्रिको फन्को मार्यो । पढ्दै जादा छर्लंग भयो — यो सबै आर्किमिडिजको सिद्धान्त राम्रो संग नबुझेकोले भएको रहेछ । एक छिन हातले मुख छोपेर बसें — राम्रोसंग बिज्ञान नजानेकै कारणले राष्ट्रिय दैनिकको मुखपृष्ठमा समाचार बन्नु — त्यो पनि सदियौं देखि राम्रोसंग स्थापित बिज्ञानको चुनौती दिंदै जसको आधारमा तरलको घनत्त्व नाप्ने उपकरणहरु लगायत ठुला ठुला पानीजहाज र पनडुब्बिहरु बनेका छन् । यसको लागि सहायता लिइएको रहेछ एउटा सानो, रमाइलो एक्स्पेरिमेंटको । खासमा यो ११ कक्षाको स्तरको जांचको प्रस्न हो – आर्किमिडिज सिद्धान्त बुझे-नबुझेको जाच्ने । आउनुहोस केहि चर्चा गरौँ ।
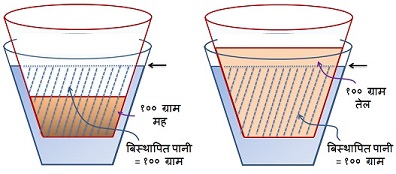
मानौं एउटा पातलो, पानीकै जस्तो घनत्त्व भएको हल्का प्लास्टिकको गिलासमा ५० ग्राम पानी छ । त्यसको माथि १०० ग्राम पानी भएको त्यस्तै गिलास हालियो भने त्यो उत्रिन्छ कि डुब्छ ? चित्रमा देखाए जस्तै त्यो उत्रिन्छ । आर्किमिडिजको सिद्धान्तले के भन्छ भने “पानीमा उत्रने बस्तुको तौल = त्यसले बिस्थापित गर्ने पानीको तौल” । परेन फसाद ? उत्रने बस्तु १०० ग्रामको, बिस्थापित हुने भनिएको पानी जम्मा ५० ग्राम । सिद्धान्त फेल खायो । २२०० वर्ष सम्म त्यत्रा बैज्ञानिकहरुले पनि कस्तो थाह नपाएका यो सिद्धान्तले काम नगरेको ?
त्यसो भए कुरा के हो त ? यो बिस्थापित पानी भनेको के हो भन्ने नबुझेर रहेछ (यो उदाहरणमा पानी लिइयो, पानीको सट्टा अरु कुनै फ़्लुड पनि हुनसक्छ)। अहिले त त्यो लेखको सबै कुरा सम्झिन सकिन तर ब्याख्या नगरीए पनि आर्किमिडिजको सट्टा एउटा नयाँ सिद्धान्त निकालिएको जसको प्याटेन्ट समेत दर्ता गर्ने भनिएको थियो । हुदै नभएको नयाँ सिद्धान्तको आधारमा यति सम्म दाबि गरिएको थियो कि नेपालको जल-विद्युत क्षमता अब १००० गुणाले बढ्ने छ ।
अलि सजिलो भाषामा बुझाउने कोशिश गर्छु — अर्किमिडिजको सिद्धान्त अनुसार बिस्थापित पानी भनेको के हो त ? मानौं तपाइँसंग एउटा सानो काठको ब्लक छ, त्यो पानीमा उत्रिदा केहि भाग पानी भित्र पनि डुबेको हुन्छ । पानी भित्र कति डुबेको छ थाह हुने हो भने त्यो पुरै काठको तौल ठ्याक्कै निस्किन्छ, सजिलै । कसरि ? त्यो पानी भित्र डुबेको भाग बराबरको पानीको तौल जति हुन्छ, पुरै काठको तौल त्यतिनै हुन्छ । डुंगा चढ्दा डुंगाको भाग पानी भित्र त्यत्ति डुब्छ जति बराबरको पानीको तौल डुंगा र मान्छेको तौल हुन्छ ।
भने पछि, आर्किमिडिज को सिद्धान्त भनेको “पानीमा उत्रने बस्तुको तौल = त्यसको डुबेको भाग बराबरको पानीको तौल” । डुबेको भाग बराबरको पानीलाइ बिस्थापित पानी भनिन्छ । यदि बस्तु अलि खदिलो छ र यसको पुरै भाग पानी भित्र हुँदा पनि त्यो बराबरको पानीको तौल कम हुन्छ भने त्यो बस्तु डुब्छ ।
अब चित्रमा हेर्नुस, पानी भित्र कति भाग डुबेको छ ? त्यत्ति डुबेको छ जसमा १०० ग्राम पानी अटाउँछ । त्यसो भए डुबेको भाग बराबरको पानी — जुन बिस्थापित पानी हो — त्यो पनि १०० ग्रामकै हुने भयो । गिलासको आकारले गर्दा पहिलो गिलासमा थोरै पानी भए पनि डुब्ने भाग त धेरै नै हुन्छ (गिलास पातलो भएको र पानीकै जस्तो घनत्त्व भएकोले बाहिर र भित्रको पानीको सतह एउटै लेभलमा हुन जान्छ) । अलि बढाई-चढाई भन्नु पर्दा १ ट्यांकर पानीमै एउटा पानीजहाज उतार्न सक्नुहुन्छ यदि पानीको एकदमै पातलो पत्रले घेर्ने गरि डुबाउने हो भने ।
पानी भन्दा अलि बढी घनत्व भएको १०० ग्राम मह राख्नुहुन्छ भने पनि त्यत्तिनै पानी बिस्थापित हुनुपर्छ उत्रनको लागि । तर महको घनत्व बढी भएकोले पानीले जति ठाउँ ओगट्दैन, अलिकति हावाले लिन्छ ( खासमा डुबेको भागमा परेको हावाको तौल + महको तौल = १०० ग्राम हुन्छ)। पानी भन्दा कम घनत्व भएको १०० ग्राम तेल राख्नु हुन्छ भने पानी भन्दा बढी ठाउ लिन्छ, तर १०० ग्रामकै पानी बिस्थापित गरेको हुन्छ ।
त्यसैले यो अर्किमिडिज सिद्धान्त पुष्टि गर्ने एउटा राम्रो एक्स्पेरिमेंट हो — न कि त्यसलाइ चुनौती । यसको गलत ब्याख्या गरेर बढाई-चढाई गरेका कुराहरु सब हावा कुरा हुन् ।
आर्किमिडिजको सिद्धान्त राम्रो संग जान्ने कोहि न कोहि त पक्कै थियो होला नेपालमा । दुखको कुरा — पत्रिकाहरुले सहि गलत जाच नगरी हेडलाइन बनाइदिन्छन । समाचार गलत भएको जानकारी दिंदा पनि खुट्टा तान्न खोज्यो भन्ने सोचिन्छ । तर यसको शिकार प्रस्नकर्ता त हुन्छ नै तर साथसाथै शिकार हुन्छ नेपालको बिज्ञानको स्तर र यसको विश्वसनीयता । हो देशमा कसैले राम्रै काम गरेकोमा प्रोत्साहन गर्नै पर्छ तर गलतलाइ अतिरन्जित गर्दा अन्तर्राष्ट्रिय बेइज्जति कमाइन्छ । विज्ञानका फोरमहरुमा यस्ता कुराहरु कुरा उचालिंदा नेपालको बिज्ञानको स्तर भनौँ या पत्रिकाको स्तर– एउटा हासोको बिषय बन्छ । साथै बिश्वास गुमाउंदै जाने हो भने नेपाल भित्रै सरकारी या जनस्तरको सहयोग पनि बिज्ञानको क्षेत्रले गुमाउंदै जान्छ ।
अन्तमा भन्नु पर्दा यो कुरा जसले उठायो, ति युवा पूर्ण रुपमा गलत हैनन् — यस्ता कुराहरु केहि ज्ञान भएको जिज्ञासुले नै गर्छ — म सरहाना गर्छु । कुनै पनि कुरामा जिज्ञासा राखेर प्रस्न गर्नु नै अनुसन्धानको शुरुवात हो र बिज्ञानको बिकासको शुरुवात हो । यस्ता युवाहरुनै भोलि केहि गर्न सक्छन । तर हाम्रोमा खाँचो छ — राम्रो मेन्टरिंगको (या गाइडको) र साथसाथै संयमको पनि । कुनै कुराको भब्य प्रचार गर्नु भन्दा पहिला आफ्नो धरातल पनि हामीले बुझ्नु पर्ने हुन्छ । भोलि गएर आफु गलत निस्कियो भने जति माथि चढेको हो उति माथिबाट पछारिन्छ । नयाँ कुरा निकाल्दा कसैलाइ चुनौती नै दिनु पर्छ भन्ने पनि नठानौं । त्यसैले साना खुट्किलाबाट शुरु गरौँ, सक्ने भन्दा बढी, अतिरन्जित दाबि नगरौं । नयाँ बैज्ञानिक खोजको प्रचार ख्याति प्राप्त जर्नलमा छापेर गरौँ, आफूखुशी पत्रकार सम्मेलनमा नगरौं । यस्ता ठुलै दाबिहरु आउँदा पत्रिकाहरुले पनि बिज्ञान प्रतिष्ठान या कम्तिमा किर्तिपुरका बैज्ञानिकको राय लिएर मात्र हेडलाइन बनाउदा राम्रो । त्यसो भयो भने पत्रिकाको विश्वसनीयता पनि रहने हुन्छ भने भविष्यमा “स्कूल पढ्ने युवाले आइन्स्टाइनको सिद्धान्तलाइ चुनौती” भन्ने कुनै पुष्टि नभएको खबर सुन्नु पर्ने छैन | ए पख्नुस, त्यो पनि सुनिसक्या हो त । स्कुले उमेरमै आइन्स्टाइनको जनरल रिलेटिभिटी पुरै बुझ्न त असम्भब जस्तै हुन्छ भने चुनौती नै दिने त कुरै नगरौं । जसलाई भेक्टरको राम्रो ज्ञान हुन गार्हो हुन्छ, त्यो लेवलको “टेन्सर” गणित लगाएर, बुझेर, छिचलेर गल्ति फेला पार्नु या अन्य व्याख्या गर्नु सजिलो छैन | कहिँ कसैले यस्तो चमत्कार गर्न सकेकै रहेछ भने बैज्ञानिक समुदायले पनि पत्याउनु पर्यो, नत्र नजानेकै मान्छेको सामु त जे बोले पनि भैहाल्यो ।
त्यसैले राम्रो मेन्टरिङ्ग र गाइड हुने र जिज्ञासा राख्नेहरु पनि उपलब्ध बिशेषज्ञहरु संग राय लिदै अघि बढ्ने हो भने तिक्ष्ण दिमागका युवाहरु हाँसोको पात्र बनेर आफ्नै भबिष्य खतरामा नपारी सहि बाटो तिर डोरिन सहयोग हुन्थ्यो जसले गर्दा उनीहरुको मात्र नभई देशको पनि भलो हुन्थ्यो। Published on: Apr 2, 2014 @ 0:16
शंकालुहरुका लागि अपडेट
(Apr 8, 2014 @ 11:06)
यो बिषयलाइ चासो दिई साथ दिनुभएकोमा सबैलाई धन्यबाद । कमेन्टहरु पढ्दा पाठकहरुलाई जम्मा ३ ग्रुपमा राख्न सकिने रहेछ:
१) पहिले नै सबै बुझेर कन्सेप्ट पनि राम्रो भएका (धेरै जसो)
२) अलि अलि पहिलै बुझेका र लेखले झन् छर्लंग भएका
३) अलि अलि बुझेका तर कन्सेप्ट राम्रो नबसेकोले अझै पनि शंका गर्ने र प्रतिकार पनि गर्ने ।
लेखको आशय “बिस्थापित पानी” के हो भन्ने बुझाउने थियो तर स्कुल तिर पढेको उदाहरणमा मात्र भर पर्दा अझै शंका रहेको लाग्यो। स्कुल तिर आर्किमिडिजको सिद्धान्त बुझाउने एउटा राम्रो उदाहरण — एउटा पानीले भरिएको भाँडोमा कुनै कुरा डुबाउने, त्यसो गर्दा चुलिएर बाहिर निस्केको पानीलाइ जोख्ने, त्यहि नै बिस्थापित पानी हो ।
यो घनत्वको र हिसाबमा ज्ञान कम भएका बिद्यार्थीहरुलाई बुझाउन प्रयोग गरिन्छ, जस्तै ७ -८ कक्षाका बिद्यार्थीहरुलाइ । यस्तो उदाहरण लिंदा पानीले भरिएको भाँडोमा प्रसस्त पानी हुनुपर्छ । बस्तुले ओगट्ने ठाउ जति पनि पानी भएन भने बिस्थापित पानी थोरै हुन्छ, अनि बस्तु डुब्छ। त्यहि भएर संधै बाहिर चुलिएको पानी नै बिस्थापित पानी हुँदैन । क्याम्पस स्तरमा आर्किमिडिजको सिद्धान्त प्रयोग गरी उर्ध्वचाप निकाल्दा लेखमा पहिला नै ब्याख्या गरे जस्तै बिस्थापित पानी भनेको पानी मुनि परेको बस्तुको भाग बराबरको पानीलाई लिइन्छ ।
स्कुलदेखि क्याम्पससम्मका शिक्षकहरुलाई छर्लंग होस् र आर्किमिडिज सिद्धान्तको गलत कन्सेप्ट नरहोस् भनेर मैले दुइ वटा चित्रहरु राखेको छु । पहिलो चित्रले नै कन्सेप्ट छर्लंग भयो भने दोस्रोमा समय फाल्नु पर्दैन ।
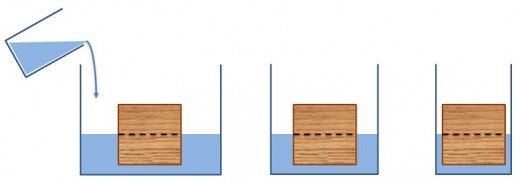
१) एउटा भाँडोमा एउटा काठको टुक्रा राख्नुस । बिस्तारै बाहिरबाट पानी भर्दै जानुस । जब बिस्थापित पानी (डुबेको भाग बराबर) को तौल काठको तौल संग बराबर हुन्छ, काठ उत्रन्छ । काठको टुक्राको सट्टा पहिला ब्याख्या गरिएको गिलासको प्रायोग गर्ने हो भने — पहिला एउटा पातलो, हल्का प्लास्टिकको डब्बामा अलिकति पानी राख्नुस, बाहिरको अर्को ठुलो भाँडोमा बिस्तारै पानी भर्दै जाने हो भने बाहिरको पानीको सतह प्लास्टिक भित्र भएको पानी बराबर हुने बित्तिकै प्लास्टिकको डब्बा चल्न थाल्छ । बाहिर जति पानी थप्दै गए पनि सतह लगभग बराबर हुन्छ, किनभने भित्रको पानी र बाहिरको पानीको घनत्त्व उही छ ।
मानौं काठको घनत्व पानीको भन्दा आधा छ । त्यसो हुँदा काठको आधा भागमात्र डुब्छ । घनत्व अलि फरक रहेछ भने अर्कै लेभलमा होला पानीको सतह । त्यहाँ चिन्ह लगाउनुस । अब अलि साँघुरो भाँडोमा यो प्रयोग फेरी दोहोरयाउनुहोस् । ठ्याकै त्यहि चिन्ह लगाएकै सतहमा पुगे पछि काठ उत्रिन्छ । यसै गरि बाहिरको भाँडो साँघुरो बनाउदै जाने हो भने काठ उतार्नलाइ कम पानी लाग्दै जान्छ, तर काठ चाही उही चिन्ह लगाएकै लेभलसम्म डुब्छ । बाहिर कति पानी छ भन्ने कुरामा यो भर पर्दैन, मात्र त्यति भाग डुब्ने गरि राख्न सक्नु पर्यो । पानीजहाज उतार्ने उदाहरण पनि यस्तै हो, बाहिर पानी थोरै भएपनि डुब्ने लेभल उति नै हुन्छ जति अरु साधारणतया हुन्थ्यो ।
२) अब यो उदाहरणले पनि बुझ्नु भएन भने गलत कन्सेप्टले नराम्रोसँग जरा गाडेको रहेछ भन्ने बुझिन्छ । यसको लागि पहिला एउटा हिसाब गर्नुस (सकेसम्म त हिसाब नराख्न खोजेको हो) — आर्किमिडिजको सिद्धान्त बुझ्न । यो हिसाब क्याम्पसको पहिलो स्तरको फिजिक्सको हो । खासमा हालैमात्र मैले बिद्यार्थीहरुलाई जांचमा सोधेको प्रस्न हो यो, यहाँ अलि सजिलो पारेर दिंदै छु :
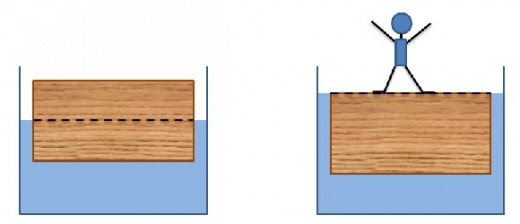
प्रश्न: एउटा पानीको ट्यांकीमा एउटा ५० kg को काठ उत्रिदा काठको आधा भाग डुबेको छ । त्यो काठको माथि कति तौलसम्मको मान्छे बस्दा उसको जुत्ता नभिजिकन उभिन सक्छ?
उत्तर:
बिस्थापित पानी निकाल्न ट्यांकीमा पहिला कति पानी छ भन्नेतिर लाग्नु भयो भने यो हिसाब हल हुँदैन । तर बिस्थापित पानी भनेको बस्तुको डुबेको भाग बराबरको पानी हो भन्ने बुझ्नु भयो भने हिसाब उत्तिखेरै निस्कन्छ ।
काठको आधा भाग डुब्दा बिस्थापित पानी = ५० kg; पुरै भाग डुब्दा बिस्थापित पानी=१०० kg. त्यहि भएर ५० kg भन्दा कम तौल भएको मान्छे उभिंदा ओभानो रहन्छ ।
फिजिक्समा हिसाब देखाउनु पर्दा : ५० kg को काठको आधा डुबेको भाग = ५० kg को पानीको भाग = (५० kg / (पानीको घनत्व ) m^3 = 0.05 m^3
बस्तुको पुरै डुबेको भाग = मान्छे सहित बिस्थापित पानीको भाग = २ x 0.05 m^3 = 0.1 m^3
(काठको तौल + मान्छेको तौल) = बिस्थापित पानीको तौल = पानीको घनत्व X बस्तुको पुरै डुबेको भाग X g = १००० X ०.१ X १० = १००० N (यसलाई Buoyant force भन्छन) । बोलीचालीमा हामी N भन्दा पनि kg मा बुझने भएकोले १००० N तौल बराबरको पिण्ड १०० kg भयो । त्यसैले मान्छे ५० kg भन्दा तल भयो भने नभिजीकन उभिन सक्छ ।
अब भन्नुस, बाहिरको ट्यांकीमा कति पानी थियो भनेर किन चाहियो ? यो आर्किमिडिजको सिद्धान्तको फर्मुलामा कहीं प्रयोग भएको छैन । त्यसैले साँघुरो ट्यांकीमा १०० kg पानी नै हुनुपर्छ भन्ने छैन, ट्यांकीमा बस्तु डुब्ने जति मात्र पानी भए पुग्छ । आशा छ, अब चाही यसमा शंका नरहला ।
यो अर्किमिडिजलाई चुनौती दिने महानुवाव ले बिस्थापित पानि भनेको कुनै बस्तु पानीमा राख्दा छेउछाउ तिर जाने पानि लाई भन्नु हुन्छ . उहाँको बिस्थापित पानीको परिभाषा अनुसार कुनै एउटा बस्तुलाई पानीले भरिएको सानो भाँडोमा दुबाउडा थोरै पानि बिस्थापित हुन्छ अनि त्यहि बस्तुलाई ठुलो तलाउमा दुबाउडा धेरै पानि बिस्थापित हुन्छ. उहाँले उर्ध्वचाप = पानिमा रहेको बस्तुको तौल (यदि त्यो बस्तु उत्रेको भए), या त्यो बस्तुले गुमाउने तौल (यदि त्यो बस्तु डुबेको भए) मान्नु हुन्छ.
त्यहि भएर उहाँले प्रयोग गर्दा कुनै बस्तु कति पानिमा डुबायो त्यहि अनुसार उर्ध्वचाप कहिले बिस्थापित पानीसंग बराबर हुन्छ, कहिले बढी हुन्छ, अनि कहिले घटी हुन्छ. त्यहि भएर ठुलो ताल मा सानो बस्तु डुबाएर परिक्षण गर्दा बिस्थापित पानिको तौल उर्ध्वचाप भन्दा २१९१ x १०^८ गुणा बढी देखिन्छ.
source: http://www.facebook.com/prcbk.
a=b हुन्छ भनि प्रमाणित गर ,
हामीलाई थाहा छ /
-ab=-ab
अथबा , a^2-2.a (a+b)/2=b^2-2.b (a+b)/2
दुवै तर्फ (a+b)/2 को hole squire जोड्दा,
अथवा , a^2-2.a (a+b)/2+ {(a+b)/2}^2=b^2-2.b (a+b)/2+{(a+b)/2}^2
अब हामीलाई थाहा छ, (a-b)^2= a^2-2ab+b^२ हुन्छ /
अथबा, {a -(a+b)/2}^2={b-(a+b)/2}^2
दुवै तर्फ squire root लिदा,
अथबा, {a-(a+b)/2}={b-(a+b)/2}
दुवै तर्फ -(a+b)/2 घट्दा वा काट्दा
a=b हुन्छ / यो तरिका प्रयोग गर्दा हरेक अंक एक अर्का संग बराबर हुन आउछ /
१=२, २=३ ७=९ जे बनौन सकिन्छ / तर यहाँ सानो गल्ति छ त्यो भनेको + वा – चिन्ह प्रयोग को गल्ति नै हो भन्ने हामीलाई लागिराछ /
this guy is really stupid to challenge the theory or archimedes principle and more embaressing fact is someone took time to take his stupidity as a news article.
send this guy back to do SLC again so he can start with basic square roots and understand what volume actually means.
doesnt matter what kind of material or how much material u put in a cup and submerge in another cup displace water it will displace the same amount since its not the material thats displacing water its the volume of the cup .
(4-9/2)^2 = (5-9/2)^2 यसमा कुनै शंका छैन ।
जब वर्गमूल निकालिन्छ त्यति बेला माइनस/प्लसको ख्याल राख्नु पर्छ । माथिको सर्वसमिकाबाट ^2 मात्र हटाएर वर्गमूल निकालेको देखाउँदा बायाँ पक्ष (4-9/2) अर्थात् -1/2 (माइनस) हुन आउँछ भने दायाँ पक्ष (5-9/2) अर्थात् +1/2 (प्लस) हुन आउँछ । त्यसैले दुवैतर्फ या त माइनस आउने गरी मिलाउनु पर्छ या त प्लस आउने गरी । यसको लागि माथिको सर्वसमिकालाई तल देखाइए अनुसार पुनर्लेखन गर्ने ।
पहिलो विकल्प: (9/2-4)^2 = (5-9/2)^2
अब वर्गमूल निकाल्दा झुक्किइन्न ।
दोस्रो विकल्प: (4-9/2)^2 = (9/2-5)^2
यसो गर्दा पनि झुक्किइन्न ।
समिकरणजस्तै हल गर्ने हो भने तेस्रो विकल्पको एक नुमना तल दिइएको छ ।
तेस्रो विकल्प: बायाँ पक्षको (4-9/2) लाई unknown ‘x’ मान्दा समिकरण x^2 = (5-9/2)^2 बन्दछ । अब वर्गमूल निकाल्दा x = ± (5-9/2) पाउँछौं ।
अर्थात् x = +(5-9/2) = +1/2
र/वा x = -(5-9/2) = -1/2
यदि हामीलाई x को मान बारे कुनै पूर्व जानकारी छैन भने x = ± 1/2 मै हिसाब टुंगिन्छ । तर यहाँ त हामीले x = (4-9/2) = -1/2 मानेका थियौं । त्यसैले x को दुइटा मानमध्ये +1/2 चाहिँ extraneous solution देखिन आउँछ । स्मरणीय यो छ कि बायाँ पक्ष बराबर दायाँ पक्ष निकाल्दैमा कामकुरो सकिँदैन । त्यसबाट आउने निष्कर्ष पनि अर्थपूर्ण हुनु पर्दछ । अर्थपूर्ण नभए हिसाब सरलीकरण गर्दा कतै त्रुटि हुन गएको संकेत हो ।
केही मित्रहरूले 4 = 5 को सट्टा -1/2 = +1/2 दाबी गर्नुभएको छ । यदि 4 = 5 हो भने दुवै पक्षमा 4.5 घटाउँदा -1/2 = +1/2 आउँछ अर्थात् दुवै निचोड (त्रुटिपूर्ण भए तापनि) समान हुन् ।
हिसाब सरलीकरणको क्रममा वर्गमूल निकाल्दा माइनस/प्लस बारे ख्याल राख्नु पर्दछ । प्राय: वर्ग गरेर वर्गमूल निकाल्दा extraneous solution देखापर्दछ ।
* * * * * * * * * * * * * * * *
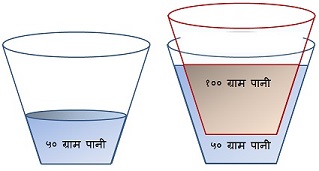
कुनै कप A मा 50gm पानी छ । अर्को कप B मा 100gm पानी छ । प्रश्न छ – कप B लाई कप A मा राख्दा के हुन्छ ? कप A तैरन्छ ? कप A ले कप B को पिँध छुन्छ ? कप A बाट केही पानी पोखिएर जान्छ ?
माथि चित्रमा देखाए अनुसार प्रत्येक कपमा 150gm भन्दा बढी पानी अट्ने देखिन्छ । सजिलोको लागि 50gm पानीको आयतन V छ भनेर मान्दा 100gm पानीको आयतन 2V हुन्छ । कपको क्षमता चाहिँ 5V मानौं । 50gm पानीमा 100gm पानी मिसाउँदा जम्मा ओगटिने आयतन 3V मात्र हुन्छ । यस हिसाबले कप A बाट पानी पोखिँदैन तर कप A मा भएको पानीको सतह चाहिँ बढेर जान्छ तैपनि कपको मुखभन्दा तल नै हुन्छ । कप A मा पानीको सतह कतिले बढ्छ त ? कप B ज्यादै पातलो छ र तौल नगण्य छ भने कप A मा 150gm पानी हुँदा पानीको सतह जति माथि हुन्छ त्यति नै माथि पुग्छ । माथि दाहिने चित्रमा जम्मा 150gm पानी देखाइएको छ । एकक्षणको लागि कल्पना गर्नुहोस् कप B (रातो घेराले देखाइएको छ) छैन अर्थात् रातो घेरा मेटाइदिनुहोस् । अब तपाईँले पाउनुहुन्छ कप A मा 150gm पानी । 150gm पानीको सतह कप A को कति माथि पुग्छ प्रष्ट हुन्छ ।
मित्र कमलजी केमा अल्मलिनुभएको छ भने 50gm पानीले (जसको आयतन V छ) कसरी 100gm पानीलाई (जसको आयतन 2V छ) विस्थापित गर्छ । कप A मा कप B राख्दा कप A को पानीको आकार बद्लिन जान्छ । आकार कतिसम्म र कस्तोसम्म बद्लिन्छ त ? कप A मा भएको पानीले 100gm पानीको लागि ठाउँ/आयतन यस्तरी “छोडिदिन्छ” कि 50gm पानी अब आएर दुइ कपको पिँधहरू बीच र भित्ताहरू बीच “चेप्टिन” पुग्छ । अन्तत: 50gm पानीले बीच भाग 100gm पानीको लागि ठाउँ उपलब्ध गराउँछ आफू “छेउभित्ता” लागेर ! यति गरेपनि कप A को पानीको आयतन चाहिँ उही 50gm नै रहन्छ (नपोखिएको कारण), मात्र आकार बद्लिएको छ । यसमा 50gm र 100gm बीच कुनै सरोकार देखिन्छ र ? त्यसैले कपमा 5kg पानी अँट्छ (बाल्टिन उपयुक्त होला 🙂 ) भने कप B मा पानी थपेर 4kg पुर्याए पनि कप A को 50gm पानीले कप B तैरन्छ । त्यति हो कप B का भित्ता र पिँधले कप A का भित्ता र पिँधलाई छुनै लागेका हुन्छन् । याद रहोस् कप मात्रको तौल र आयतन (पिण्डको मात्र) नगण्य ठानिएका छन् । यसलाई अर्को तरिकाले यसरी बुझ्न सकिन्छ । कप A मा 4kg + 50gm पानी भर्नुहोस् । अब काल्पनिक कपको रेखाङ्कन गर्नुहोस् जसमा ठ्याक्कै 4kg पानी होस् । त्यो काल्पनिक कपले झण्डैझण्डै कप A को पिँध र भित्ता छोएको पाउनुहुन्छ तर तैरिकएको अवस्थामा पाउनुहुन्छ, होइन र ?
यदि कपमा 130gm मात्र पानी अँट्छ भने 100gm पानी भएको कप B को कारण कप A बाट 20gm पानी पोखिएर जान्छ । अब कप A मा बाँकी रहेको 30gm पानीमा कप B तैरन्छ कि चुर्लुम्म डुब्छ ? कल्पना गर्नुहोस् कप A मा 130gm पानी छ । अब काल्पनिक कप B रेखाङ्कन गर्नुहोस् जसमा 100gm पानी होस् । काल्पनिक कप B पिँधसम्म डुबेको पाउनुहुन्छ र ?
पानीको सट्टा कुनै malleable धातुलाई उदाहरण लिएर मास्तिरको अनुच्छेद प्रष्ट हुन्छ । धातुको एउटा टुक्रा A को शुरु आकार cube को छ जसको आयतन 2x2x2cc अर्थात् 8cc छ । अर्को टुक्रा B पनि cube आकारको छ जसको आयतन 4x4x4cc अर्थात् 64cc छ । दुवै टुक्राको आकार उही रहे A भित्र B अँट्दैन । अब टुक्रा A बाट ढकनी बेगरको बाकस (चार भित्ता र पिँध भएको तर छत नभएको) बनाऔं । यसको लागि टुक्रा A लाई निकै पातलो हुने गरी पिटेर सतह चाहिँ एकदमै फराकिलो बनाउनु पर्दछ । बाकसको लम्बाइ 5cm, चौडाइ 5cm, उचाइ 5cm बनाउँदा भित्ता चाहिँ 8/125cm पातलो (वा बाक्लो) हुन आउँछ । अब यो बाकसमा टुक्रा B सजिलै अँट्छ । पानी र धातुका उदाहरणहरू ठ्याक्कै नमिले पनि कसरी थोरै पानीले धेरै पानीको लागि खालि ठाउँ उपलब्ध गराउन सक्छ भन्ने जानकारी दुवै उदाहरणहरूले दिन्छन् ।
तपाईको लेख राम्रो लाग्यो | तर यसले law of floatation र आर्किमिदिजको सिधान्त लाइ कसरि ब्याख्या गर्यो मैले बुज्न सकिन |
आर्किमिदिज को सिधान्त ले के पनि भन्छ भने विस्थापित पानीले बराबरको upthrust वस्तु मा दिन्छ.| तपैले भने जस्तै कप B कप A मा उत्रिन्छ येस्मा संका छैन |
अब तपाई कै कुरालाई यहाँ दोहारौं कप B कप A माथि उत्रिएको छ | कप B को कारण ले कप A को पानि को आकार बदलिएर दुवै को सतह को पानि बराबर उचाई मा छ | यसलाई हामी येसरी बुझ्न सक्छ वा यसरि एकचोटी बुझौं | कप B को पानी कप A को पानीमा मिसिएको छैन भनि सोचौं (घनत्व बराबर भएको बेला तपैले काल्पनिक रेखा छ भने जस्तै यो कुरा मान्न सकिन्छ ) | भनेपछि विस्थापित हुने पानी भनेको कप A को मात्र हो | तर कप A को पानी जम्मा 50gm मात्र छ | अर्थात् एसले बढीमा 50gm को वा त्यहि अनुसार को upthrust कप B मा दिन सक्छ | तर कप B ले तल तिर दिने बल 100gm को हुन्छ |
अनि कसरि 100gm पानी 50gm मा उत्रिन्छ भन्ने ?
त्यसकारण माथि दिएको प्रयोग सहि भएपनि तपाई र बिज्ञान बा को लेख ले पूर्ण र संतुस्ता व्याख्वा गरेको छ जस्तो मलाई लाग्दैन ? कमल र ज्ञान ले येही भन्न खोजेको जस्तो लाग्छ |
As far as I guess you are completely clueless about what Archimedes Principle says actually says. However this should be useful for many people and I am expressing it quantitatively.
Upthrust = dgV . Where V is the volume of the floating object that is under the surface of the floating liquid, d is density of the fluid, and g is acc. due to gravity.
Here volume of the floating object that is under the surface of the floating liquid = 100 gm (because 100gm is floating on 50 gm of water)
Let us calculate upthrust now.
V= mass/density = 100 gm / d
Upthrust = dg(100 gm)/d = g. (100 gm)
Weight of the floating object = mg = 100gm . g.
Therefore Upthrust = Weight of the floating object.
Malekarji,
प्रश्नको लागि धन्यवाद ।
ब्लगको मूल अंशमा आर्किमिडिजको प्लावन सिद्धान्त बारे राम्ररी व्याख्या दिइएको छ । अनि विभिन्न टिप्पणीकर्ताहरूले पनि थप उदाहरण र व्याख्या गर्नुभएको छ । त्यसैले यस विषयमा मैले ध्यान दिइनँ ।
मैले त BBji र Kamalji बीच भएको लामो जुहारीको कारण मात्र टिप्पणी गरेको थिएँ । BBji ले थुप्रै प्रष्टिकरण दिनुभए तापनि कमलजीलाई 50gm पानीले 100gm पानी उचालेको (कपमा भएको कारण) शंकास्पद लागिरहेकोले मलाई थाहा भए अनुसार थप प्रष्टिकरण दिएको थिएँ । दुवै कपमा पानीमात्र भएकोले र भित्री कप ज्यादै पातलो र नगण्य तौल मानेको अवस्थामा आर्किमिडिजको प्लावन सिद्धान्त बेगर पनि व्याख्या गर्न सकिन्छ । बैसाखी बेगर हिँड्न सकिन्छ भने किन बैसाखीको भार बोक्ने ?
तपाईँको टिप्पणीबाट तपाईँमा पनि “विस्थापित पानी” को अवधारणा बारे थोरै अलमल छ भन्ने मलाई लागेको छ ।
कुनै वस्तु पानीमा तैरँदा वा डुब्दा सो वस्तुको जति अंश पानीभित्र हुन्छ त्यति आयतन बराबर पानीलाई सो वस्तुले भाँडोको “छेउभित्ता” ठेलिपठाएको हुन्छ । सो आयतन बराबर पानीको परिमाणलाई आर्किमिडिजको प्लावन सिद्धान्त अनुसार “विस्थापित पानी” भनिन्छ । यो “विस्थापित पानी”सँग भाँडोमा शुरुदेखि रहेको पानीको परिमाणसँग कुनै सरोकार राखेको देखिन्न, होइन र ? स्मरणीय के छ भने शाब्दिक रूपमै विस्थापन भएको पानी भाँडोमै हुन सक्छ (भाँडो ठूलो भएमा) वा पोखिएर बाहिर गएको पनि हुन सक्छ (भाँडो सानी भएमा) तर “विस्थापित पानी” चाहिँ वस्तुले पानीभित्र ओगटेको आयतन बराबर नै रहन्छ । त्यसैले भाँडोमा भएको पानी र “विस्थापित पानी” बीच कुनै सम्बन्ध छैन । “विस्थापित पानी” त भाँडोमा भएको पानीले तैरेको वा डुबेको वस्तुलाई कति ठाउँ/आयतन छोडिदिएको हो त्योसँग चाहिँ सम्बन्ध राख्छ ।
कपमा 50gm पानी छ भने upthrust बढीमा 50gm-wt बराबर मात्र हुन सक्छ भन्ने धारणा त्रुटिपूर्ण छ । त्यो upthrust त विस्थापित आयतन, पानीको घनत्व र गुरुत्वाकर्षण प्रवेगमा भर पर्छ ।
खुशीको खबर – एप्रिल ५ मा कमलजीले BBji को व्याख्यामा चित्त बुझाइसक्नुभएको छ ।
विज्ञान बाले थप व्याख्या गर्ने क्रममा हिसाब पनि गरेर देखाउनुभएको छ । प्रयास प्रशंसनीय छ तर पिण्ड (mass) र तौल (weight) उल्लेख गर्ने मामलामा चुक्नुभएको छ । तौल उल्लेख गर्दा या त newton लेख्नु पर्यो या त kg-wt / gm-wt (kilogram weight / gram weight) लेख्नु पर्यो । अनि कलेजको प्रश्नमा एउटा शब्द “बढीमा” थपेर “काठको माथि कति तौलसम्मको मान्छे बस्दा”लाई “काठको माथि बढीमा कति तौलसम्मको मान्छे बस्दा” बनाए ठीक हुन्थ्यो भन्ने मलाई लाग्छ ।
जाँदाजाँदै,
किस्सा १: पहिलोपल्ट स्कुल गएर घर फर्केपछि फुरुक्क भएर नेपाली फुच्चेले उसको बुबालाई सुनाएछ – बुबा, मैले त अंग्रेजीमा यहाँ आऊ भन्न जानेँ नि । बुबा मक्ख परेर स्याबासी दिँदै फुच्चेलाई सोधेछ – अनि अंग्रेजीमा बाहिर जाऊ भन त । फुच्चेलाई त्यो सिकाइएको थिएन त्यसैले एकछिन त रनभुल्ल परेछ । झिलिक्क फुच्चेको “ट्युबलाइट” बल्छ । फुच्चे खुरुरु कुदेर कोठा बाहिर गएर उसको बुबालाई भन्छ – कम हियर ।
किस्सा २: कुनै वैज्ञानिक (नाम याद भएन) कहाँ भर्खरै विश्वविद्यालय उत्तीर्ण ग्राजुएट काम गर्दोरहेछ । ऊ (ग्राजुएट) गणितमा तगडा रहेछ । कामको सिलसिलामा वैज्ञानिकले एउटा घ्याम्पोको आयतन थाहा पाउनुपर्ने भएछ । त्यसको लागि ग्राजुएटलाई अह्राइराखेर अरू काममा वैज्ञानिक निस्केछ । निकै बेरपछि ऊ फर्कँदा ग्राजुएट त घ्याम्पोको उचाइ, गोलाइ, कहाँ कति बाक्लो छ भनेर नाप लिँदै नोटबुकमा टिपोट गरिरहको हुन्छ । के गरेको भनी वैज्ञानिकले सोध्दा घ्याम्पोको उचाइ, गोलाइ आदिको नापबाट हिसाब गरी आयतन निकाल्ने जानकारी ग्राजुएटले दिएछ । दिक्क मान्दै वैज्ञानिकले घ्याम्पोमा पानी भरेछ र भनेछ – घ्याम्पोमा पानी कति छ सिलिण्डरमा पानी खन्याएर पत्ता लगाऊ ।
माथिका दुई किस्साहरूबाट सार चाहिँ आफै निकाल्नु होला । अध्यापन कार्यमा संलग्न हुनुहुन्छ भने विद्यार्थीहरूसँग गफिने खुराक पनि बनाउन सक्नुहुन्छ । 🙂
धन्यबाद परशुरामजी, सजिलोको लागि मुखैले उत्तर आउने उदाहरण राखियो, तर बीचका स्टेपलाइ बोलीचालीको भाषामा भर्न खोज्दा अलि मिलेनछ | साथै तपाइको पहिलो किस्सा रमाइलो रहेछ, त्यसको लागि पनि धन्यवाद |
I read this article four times to understand. Hya….. कुरा त अति simple रहेछ . First principle, volume of the floating body under water = volume of displaced water.
Further, Density = mass/volume
Then by first principle, floating glass displaces the equal volume of water in first glass. If the densities of the both water are equal, mass of the water in floating glass (surface levels of both glasses are same) equals to he mass of the water displaced in the first glass.
Maybe I missed something but the writer doesn’t seem to completely answer the original question. No doubt he clearly and correctly explained the archimedes principle but the issue is how can a cup with 100g water float on top of cup with 50g of water. If the cup with 100g of water is to float then it must displace 100g of water but there only 50g of water to displace. So if infact cup with 100g water was floating then this cannot be explained with Archimedes principle alone.However, are we sure that this really does happen? Does a cup with 100g of water really float on top of 50g water? Try it yourself? Maybe the claim is false in the first place.
I have not done this experiment myself but I highly doubt this really happens.
Yes, you did miss the point. It can be explained solely by the Archimedes principle. The whole argument in the present blog is that the definition of displaced water is not how much water you have in the first cup. The displaced water is in fact how much of the second cup is under water, which is shown by the shaded area. If you look at the shaded area, it is the volume of the second cup under water. Because of the shape of the cup, the water level in the first cup has to rise when you dip something in it. This raised level of water makes sure that a larger volume of the second cup is under water.
Sure, it is easy enough experiment do try out to see whether it happens. But if you know a bit about the property of liquids, liquids with same density cannot have two different levels. The water in the first cup and the second cup have the same density. So if you have light weight cup with similar density as water, the water level should be the same. It also does not matter with the shape of the container.
There are two different points in Archimedes principle:
1. The first one is very general. It applies whether the body is submerged or floating. It says that the volume of object under water is equal to the volume of water displaced. This is just common sense. If a stone sinks, it will displace equal water equal to its volume. if the object is not fully submerged then the volume of water displaced is equal to the volume of object that is under water. For instance if a wood is floating and 1/2 of its volume is under water then volume of water displaced= 1/2 the volume of wood.
2. The second one applies only if the object is floating and its called “principle of floatation” (see wiki for more detail).It says that the weight of water (or any fluid) displaced equals to the weight of the floating object. This does not apply if the object is completely submerged.
My concern was with the second point i mentioned above. If the top cup (second cup in BB’s comment) is to float it must displace water from the bottom cup equal to its weight but there is not enough water to be displaced.
@BB You reply was totally based on first point. You missed the “principle of floatation”.
Correction: When I said ” This does not apply if the object is completely submerged” in second point I mean “If the object sinks” that is if the object is sitting on the floor of the cup and is not floating.Like a coin on bottom of water cup.
You missed the point again. Your “second point” is already included in the example of the floating oil. It is not completely submerged, yet it displaces the same amount of water (shaded area) as before, which is equivalent to 100g.
I repeat again, the definition of “displaced water” is the amount taken up by the part of the object under water, whether fully submerged or partially submerged. This is exactly why first cup floats. See the reply of Sanu and Manoj below as well.
Until you understand what “displaced water” really is, you will continue to make the same mistake.
Eureka! This is what Archimedes exclaimed when he steeped into the water bath and suddenly noticed the water level rose. He realized that the volume of displaced water equal to volume of his body submerged. See, displaced water does not refer to his body. “Displaced water” means the actual amount of water that his body displaced.
Imagine you have a cup that is full of water. Its really full. Now put some object into the water. Ok, what happens? Water will spill or overflow. Collect that spilled water. That is the displaced water. Now,
if the the object you put was completely under water but not touching the bottom of the cup then the volume of the object equals the volume of the object that get spilled. Also, weight the spilled water and you will find that it will equal the weight of the object. Here both volume and mass of displaced water equal volume and mass of the object.
If the object you put was partially under water and partially over. Then the volume of spilled water (displaced water) = volume that is under water ( not the total volume) OK. Now weight the spilled water ( displaced water). You will find that the weight of the spilled water is the same as the weight of the object.
If you put a iron ball (78g with volume 10 cm^3). Since the ball has volume of 10cm^3 the volume of water spilled (displaced water) is also 10 cm^3 ( which equals 10 g).
What we mean by displaced water when talking about Archimedes principle is the spilled water. The actual displaced water. What Archimedes principle says is that this volume equals the volume of the object in water (in you case the shaded region.)
That is true only when you are spilling the water. You are still getting the wrong definition of displaced water. You will continue to make the same mistake as you are doing.
no no no. Kamal is right in definition of displaced water. spilling of water does not change meaning of the amount of water displaced. whether water spilled or not the definition is same. Displace water mean the amount of water level of the first glass raised.( level difference) if not spilled The volume of 100gm water in second glass must not be counted )
“Displaced water” means how much water you displace. Its straight forward. In this case it will be the amount of water displaced form the bottom cup. There is no Archimedes principle or anything here. Now what our common sense tells is that this volume of displaced water must equal to the volume of object under water. This is because the object has now occupied that space and to occupy that space it must displace water. I hope you get this point.
The issue about floatation has to do with weight of the object and weight of displaced water. Law of floatation says weight of the object = weight of liquid displaced. The object that is floating here is 100g of water on a cup. So from law of floatation we know that the weight of displaced water must be 100g. This is the water that the top cup must displace from the bottom cup but there is only 50g of water in the bottom cup. So that is why I am saying this is impossible. If you really try this out, the bottom of the top cup will touch the bottom of the bottom cup and the object is no more floating.
How can 100 gm water can float in 50 gram of water? Even the both have the same densities the glass with 100 gm of water still should displace the 100 gm water from another glass to float. But the second glass has only 50 gm. If two bodies have the same densities, one body (whether liquid or solid) can be placed in another liquid with same density at any position under the second liquid. But still have to displace the same volume and hence same mass (when densities are equal). But the second glass has only 50 gm of water.
Every one knows “Law of floatation ”
wt of floating body = wt of displaced liquid=volume of body under water into density of liquid
if density of 50 gm of water is equal to density of 100 gm of water and glass then
wt of diplaced liquid = volume of 50 gram into density
100gm = volume of 100 gram into density
since both have same density they are equal, at least wt of displaced liquid must of equal.
So whether the glass of 100gm water(with glass) have same density with
50 gm of water or not, 100gm of water with any glass cannot float in 50 gram of water.
Note since the acceleration due to gravity is same for all wt and mass are taken as same.
ग्यान र कमलले एकपटक यो प्रयोग गरेर हेर्नुस अनि आफ्नो व्याख्या गर्नुहोला | नत्र उत्रदै उत्रन्न, सतह एउटै हुनै सक्तैन भन्ने गेस मात्र गरेर समय नाफलेकै राम्रो, तपाइँहरु पनि त्यहि ४=५ प्रमाणित गर्दै बस्दै गर्नु भाछ | यहा मात्र यति बुझे हुन्छ कि “बिस्थापित पानी” भनेको बाहिरको पानीको सतह भन्दा मुनि परेको बस्तुको डुबेको भाग बराबरको पानी हो | ५० ग्राम पानीमा डुबाउदा पनि डुब्ने भाग त उत्ति डुब्या छ नि, त्यहि भएर बिस्थापित पानी १०० ग्राम नै भएकोले उत्रेको हो | त्यहि ५० ग्राम भनेकै बिस्थापित पानी हो भनेर अड्डी लिने हो भने तपाइलाइ कसैले बुझाउन सक्तैन |
I am getting to the point after thinking for long. BB you are right for the case when the density of the glass with 100 gm of water is equal to the density of water of 50gm only.
It is just the case adding 100gm of water in 50gm of water thinking the 100gm of water is floating in the water without mixing with each other. Am I right?
I will sure try this experiment.
@BB, Yes u are right! Good Job! Thumbs up!
Kamal ..the volume occupied by the submersed object, if filled with water, will weigh equal to the submersed object …
the best way to picture it is if a cup is filled fully with 200 grams of water and you immerse 100 gram weighed cup, it will displace 100 grams out of the full cup as that space is now occupied by the new cup.
in this case, the volume worth of 100 grams of water is now taken by new cup and the 50 grams of water is around that volume. ‘Displacement’ is the key word here
The key word according to me is floatation here. Most people and many freshman physics student get confused about principle of floatation. I already explained in reply to BB but let me try to explain this again.
If the object is floating, there are two equations to work with:
1. volume of liquid displaced = volume of the floating object that is under water.
For instance, if an object is completely submerged, then the volume of water displaced will be equal to volume of the object. However, if it is partially submerged then the volume of water displace does not equal total volume of the object but just the volume of object that is under water. I wish i could draw some pictures but sorry
2. Weight of liquid displaced = weight of object.
This is a crucial point that most people forget. We normally think an object will sink in water if it’s density is larger than density of the water. A iron pin sinks because its density is greater than that of water and a wood floats because its density is less than that of water. But, this is not the whole story?
If object with density higher than that water were to always sink then why doesn’t a ship mostly made of iron sink? The answer has to do with law of floatation. It says that an object will float if it can displace water equal to its weight. A ship is designed such that it displaces water more than its own weight so it floats. A iron pin cannot displace water equal to its weight because its volume is small. Ok, I don’t think anyone is reading upto this point, if you have then thanks for reading. Bye bye.
Sinking or floating purely depends on relative density of two liquids or liquid and the object.
Density of water = 1000 kg/m3 and density of ice = 9200 kg/m3
The ratio is 9200/1000 = 0.92 = 92%. This means 92 % by volume of ice will be under the water even though ice floats in water. If some object has density equal to the density of water then 100% of the object will be under the surface of water but up to the surface. Will the object will go into bottom of the water? No. This is the minimum condition required to float.
Now lets go to the example of iron ball and iron boat or iron ship?
The density of iron is higher than the density of water. So all iron ball iron ship or iron boat should sink in the water. However iron ship or iron boat can in some situation float in water? Does this violate the density law then? No.
The reason is big portion of the ship or boat is designed to be filled with air which lowers the average density of the ship or boat system lower than the density of water. In this condition the boat or ship will float in water.
Mathematically,
Upthrust = dgV, where d = density of water, g = acceleration due to gravity and V = volume of the object under the water.
This means upthrust depends on volume of the object under the water. When ship or boat are designed in such a way that big potion of them is filled with air upto the level of surrounding water level, the upthrust is much bigger up to the weight of boat or ship causing them to float.
Note: The volume can not be changed by changing its shape from iron ball to iron boat. This means volume of iron under the water can not be changed until its designed in a way that significant portion of it is filled with air or lighter materials simply by changing iron ball to iron coin or iron block.
BB is 100% right. The water level on both glasses should be the same (same density). This means by very common sense that 100g water should be fully under the 50g water. This means the amount of water displaced itself should be 100 g because 100g water is fully inside the 50g water. There is nothing to do with 50 gm water as long as the glass holding 50g is big and dip enough to hold at least up to the level 100g of water.
माथि सबैको अंग्रेजी गफलाई यहा एक लाइनको नेपालि कुराले सक्याउ!
‘कुनै पनि बस्तुको भार सो बस्तुको आयातन र तेस्ले वोगट्ने क्षत्रफल संग अन्तरसम्बन्धित हुन्छ!’
यहि कुराले नै बताउदछ कुन कति पानीमा उत्रन्छ र कुन दुब्दछ!
‘इसी बातामे मिलेगा कुनो कितने पानिमे है!’ एउटा धोतीले भन्ने गर्थ्यो यहा पनि लागुहुने देखियो!
100gm of water with glass fully under the water of 50 gm only ????????
Its not about being the glass with 100gm water in the glass of 50gm. It is about the floating?
परेन
फसाद ? उत्रने बस्तु १०० ग्रामको, बिस्थापित हुने
भनिएको पानी जम्मा ५० ग्राम ।
This is the main confusion n i agree that it has not been cleared in the article…
In my view, here all needed 100gm water is displaced n no doubt Archimides is right.
In the examples of comments,full glass of water n displacement shows there should b enough water to displace n thats true.
My point is, while immersing 100gm water cup into the 50gm one, the displaced water by the bottom of 100gm cup has raised its level n it is displaced again by the upper part of 100gm water cup compansating the required part.
In the example of comments,full glass of water n displacement, there is no repeated displacement n total mass of displaced water by 100gm water is 100gm.
Hope the confusion has been dilated.
And another thing, the topic of this article is about Einstein n most of the body part is about Archimides.
This is not fair…
ठगि (a – b)^2 फर्मुला मा छ | कुनै पनि शंख्याको बर्गमुल + या – हुन सक्छ | यहाँ दुवै साइडमा + लीएको छ जुन गलत हो | एक तिर + अर्को तिर – हुनु पर्थ्यो |
(4 – 9/2)^2 = – (5 – 9/2)^2
(4 – 9/2) = – (5 – 9/2)
4 – 9/2 = -5 + 9/2
4 + 5 = 9/2 + 9/2
9 = 9
(४-९/२)^२=-(५-९/२)^२
अब दुबैतिरको ^२ हटाइदिउ,
(४-९/२)=-(५-९/२)
जहिल्यै पनि पहिला ब्राकेट भित्रको कुरा समाधान गर्नुपर्छ किनकि त्यो महत्वो पुर्ण हुन्छ तेसैले ()मा राखेको हो!
९/२ भन्नु ४.५ हो!
(४-४.५)=-(५-४.५)
(-०.५)=-(०.५)
अब ब्राकेट हटाउ
-०.५=-०.५
How about this?
^2 means there are two solutions for this problem and you must choose the solution that does not violates math law. In this case +
What is the problem with -0.5 = -0.5?, isn’t -0.5= -0.5?
^२ भन्या स्क्वायर भन्या होइन र?
टु सोलुशन पो भन्या हो? तेसो भय मेरो हिसाब बिग्रियो ल!
There is no problem with -0.5=-0.5 that is why I ask you guys to find the problem.
Find the problem if you can, use your brain and tell me what is the problem.
If you don’t see then tell me you didn’t see.
ok
You have no idea what square root implies in polynomial equations. The highest degree implies the number of possible solutions on that equation. So first learn that.
x^3 = 1 means there are exactly 3 solutions for x and they are [1, -1/2+ i(√3)/2, -1/2-i(√3)/2] where i is an imaginary number √(-1) and can only be defined in complex math system. You cannot apply secondary level math in polynomial equations. So, if you do not get what I want to tell just leave it, it is not in you capability. So just study some maths. 🙂
हस, ट्युशन पढ्न आउनुपर्ला गुरुसँग,
कताहो कोचिङ्ग सेन्टर र कति पैसो फिस लाग्नेहो?
२+३= ७ हुन्छ,
हिसाब बिग्रेमा,
and Imagination मा!
हात्ती = घोडा
बाघ = कछुवा
यो पनि हुन्छ,
भनौ कसरि?
X^3=1 means there are exactly 3 solution.
What would you do if I give you 5 solutions?
X^2 means x value 2 times if this is square but if you imagine x riding on the horse.
above equation talk square not root.
चिया र कफीको कुरा हुदा पाउरोटी र बिस्कुट घुसाउने, चिया संग पाउरोटी खाइन्छ तेसैले र कफी संग बिस्कुट खान्छु म तेसैले, भनेर.
अनि पाउरोटी पाएन भने काक्रोले काम चलाउने, काक्रो चोप्पेर खाउ, जस्त इमाजिन भन्ने?
May be you are tough in math and challenge Archimedes or Galileo but I’m definitely not. I’m just talking simple solution of above equation.
आफुलाई खुबै जान्ने ठानेर अर्को लाइ पढ्ने अर्ति पनि दि नहाल्नेकी साथि!
साथि माथि
Lol so you want to give me 5 solutions of x^3 = 1. 😀
This proves you do not know anything about Higher Level Mathematics. I cannot teach idiots who can challenge to give me 5 solutions of x^3 = 1. So sorry no tuition. Now, I understand why people say “Do not argue with an idiot. He will drag you down to his level and beat you with experience” because there are people who claim to give 5 solutions of x^3 = 1.
नेपालमा मात्रै किन धेरै Einstein लाई चुनौती दिन्छन ? भबिन्द्रको कुराले हाँसो लाग्यो अनि mentor को अभाब त पक्कै नै छ नेपालमा |
Teacher QUESTION:
Prove that: 4=5
Student ANSWER:
LHS = 4
RHS = 5
LHS x 0 = 0
RHS x 0 = 0
Therefore, LHS=RHS Proved//
Teacher MARKS SCORE:
(80/80) X 0
= 0
( :p Just for Fun )
Last step ma mistake chha
4-9/2=5-9/2
Result would be
(8-9)/2=(10-9)/2
-1/2=1/2
-0.5=0.5
If you take square-root both side
it would be
0.25=0.25
then multiply by -80
it would be
-20 = -20
१. नेताहरुको हावा गफ छापिने पत्रिकामा बिज्ञान अनुसन्धानको समाचार पढेर मख्ख पर्नु गलत हो !
२. बिज्ञान अनुसन्धानको समाचार राष्ट्रिय दैनिकमा होइन science journal हरुमा छपाउनु पर्छ, बैज्ञानिक हुन चाहनेले र पढ्न चाहनेले पनि science journal खोजेर पढ्नु पर्यो ! अहिले त सबै जोउर्नलहरु online नै छन् !
उदाहरण: http://www.nature.com
जति बराबर जति पनि आइहाल्छ नि. x .0 =y .0 गर्दियेसी. इनिहरु सबै येस्तै येस्तै बकबास कुरा हरु का प्रयोग हुन्.
लिमिट को हिसाब गर्दा येस्ता उदाहरण कति छन् कति उसैले अनन्त उत्तर आउछ हिसाब गर्दै जादा फेरी नुमेरिकल उत्तर आउछ इनि हरु सबै साधारण हिसाब हरु हुन्
त्यो क्यासेट को मोटर र ब्याट्री हालेर हेलिकोप्टर बनायो भनेर ठुलो बैज्ञानिक भयो भनेर हेड लाईन बनाउने, अनि फेरी त्येस्तै कुरा लै प्रोत्साहित हुने गरि कमेन्ट गर्ने लै पनि हेलिकोप्टर को बारेमा कुरो भुझने गरि लेख लेखौ त बिज्ञान बा, जति चोटी त्यस्तो समाचार आउछ, त्यति नै कन्सिरी तात्छ मेरो त.
आफुले नि कुनै जमानामा क्यासेट त हैन, अरु खेलौनाको मोटर निकालेर प्लेन बनाइएको थियो/ तर ब्याट्री भारी भएकोले ऊद्न चै ऊदेन , अगाडी दौडे पनि / घरमा चाही खेलौना बिगार्यो भनेर गाली खाइएको थियो /
धन्न कुनै पत्रिकाले चाही देखेन, नत्र राइट ब्रदर्सलाइ challenge गर्ने बैज्ञानिक भनेर छापिसक्थ्यो होला/
I hope that these news are not published in English. Otherwise my colleague will make fun of my PhD degree in Physics.
Looks like you are the one who wrote that stupid article, otherwise why would you worry about being teased by colleague? Or did u do your PHD in physics from Nepal? You sounds such a jocker.
राजनीति गफ भोजन गरिरहेका लाइ बेला बेला मा बिज्ञान गफ पस्किदा राम्रै रुचाएको देखिन्छ |
येस्तै कहिले हास्य व्यंग पस्कनु , कहिले साहित्य , कहिले कला , कहिले मनोरंजन |
अंक गणितमा ज्यामिति र विजगणितको root square प्रयोग गर्न पाईँदैन।
Physicists are doing research and trying hard to explore the mystery behind cosmos via black hole, dark matter/energy, antimatter, multiverse, antigravity and we are trying to act ‘over-smart’ with our stupid elaboration.
(No offense)
Similar One!
2=2
2^2=2^2
2^2-2^2=2^2-2^2
use a^2-b^2=(a+b)(a-b) on left side, take 2 common on right!
(2-2)(2+2)=2(2-2)
(2-2) cancel from both sides!
2+2=2
4=2
Enjoy!
You cannot cancel (2-2) from both sides.
because you can cancel (a-b) from both sides iff
(a-b) is not equals to 0
To cancel (a-b)/(a-b), denominator must not be 0.
And in your case it will be 0/0 which is indeterminate form. Even Chinese calculator detects 0/0 as error.
I appreciate your effort to explain the principle in our language in simple words. However, I don’t think that you gave the true reason why the 100 g water cup floats in 50 g water cup. As long as there is no other way for water to go out of the cup, level rises and so the pressure too. The increase in pressure then increases upthrust and that is why the cup floats. Please correct me if I am wrong 🙂
It is the true reason. The buoyant force is equal to d*V*g (density of water x Volume under water x Acc. gravity).
If you calculate the buoyancy based on the pressure difference, you will get exactly the same answer. Here is how: the pressure at the bottom of the glass is d*g*h (density x gravity x height). Pressure x Crosssectional area = Force. Here cross-sectional area as well as the pressure changes as you go up from the bottom. So to calculate the total force, you have to integrate d*g*h x A by taking small increments in height, which is dh. Here density and g are constant, so if you integrate Adh, you get the total volume V, which will give you the original buoyant force d*V*g.
यो ABCD वाला फर्मुलाहरु निकै घोकियो उ बेलामा…..कुरो बुझेको भए मार्दिनु!!!!!! त्यहि भएर होला लेखक ले अलि सरल भाषामा बुझाउन खोजेको!
Achut जी तलको link को Upthrust and Archimedes principle पढ्नुस –
http://www.schoolphysics.co.uk/age11-14/Matter/text/Archimedes_/index.html
एउटा कुतर्क “अलि बढाई-चढाई भन्नु पर्दा १ ट्यांकर पानीमै एउटा पानीजहाज उतार्न सक्नुहुन्छ यदि पानीको एकदमै पातलो पत्रले घेर्ने गरि डुबाउने हो भने ।” कस्तो अनि कुन तरिकाले पातलो तहको कुरा निस्कियो?
बिज्ञान बा को यो उदाहरण अलि चित्त बुझेन. कुरा एकदमै सफा अनि प्रस्ट थियो तर पनि लामो नचाहिने धेरै उदाहर्ण दिनु पर्ने थिएन. त्यो १०० ग्राम वाला गिलास पक्कै पनि डुबेको हुन्थियो येदि त्यो गिलासमा १०० होइन ५१ ग्राम मात्र भए पनि तर पानी बिट सम्म हुनु पर्थियो अर्थात् तेत्ति मात्र पानी अट्ने गिलास हुनु पर्थियो तर गिलासको घनत्वो पानी बराबर वा त्यो भन्दा बढी भएको खण्डमा. त्यो भाईको कुरो केहि हद सम्म सहि हो लाग्न आएको किनकि यहाँ किन डुबेन भन्ने मात्र नभई अनि किन १०० ग्राम पानीले ५० ग्राम पानी समेत बिस्थापित गर्न सकेन भन्ने पनि हो. बिज्ञानबाको तर्क सहि भए पनि संधर्ब अनुसार पूर्ण छैन किनकि बिज्ञान बाले गिलासको बिटको कुरा कहिँ कतै गरेनन. एउटा ५० ग्राम पानी मात्र अट्ने गिलासमा भरिपानी राख्नुस अनि तेही साइज को गिलास मा ५१ ग्रामको ढुंगा, पानी वा कुनै पनि चिज राख्नुस त्यो पुरै पानी बिस्थापित हुनेछ वा डुब्ने छ वा चित्रकै जस्तो गिलासमा ५० ग्राम पनि राख्नुस अनि बिट सम्म भरिने गरि 51 भन्दा माथिको तौल बराबर पानी राख्नुस यो पटक पनि त्यो गिलास उत्रिने छैन. अर्किमिदीजको सिदान्त बुझ्ने हो भने येसो पनि गरि हेर्नुस. एउटा ठुलो बाटामा अर्को मझौला बाटा राख्नुस माथिको मझौला बाटामा पूर्ण रुपमा भरिने गरि पानी भर्नुस अनि पानीमा तैरिने गरि एउटा खाली कसौडी राख्नुस.त्यो कसौडीले आफ्नो तौल बराबरको पानी बिस्थापित गर्ने छ फेरी तेस कसौडी माथि ५०० ग्रामको ढक राख्नुस त्यो कसौडी अझै तल सम्म डुब्ने छ र अर्को ५०० ग्राम पानी बिस्थापित गर्ने छ. तौल थप्दै जानुस अनि हेर्नुस.कसौडीले आफ्नो खुद तौल अनि थपिएको सम्पूर्ण तौल बराबरको पानी बिस्थापित गरेर मात्र डुब्ने छ. बिस्थापित पनि तौली हेर्नुस.( १००% accurate नहोला ) ट्यांकरको पानीमा जहाज उतार्ने हो भने पातलो तह होइन गहिरो भाडामा पानी राख्नु पर्ने हुन्छ र जहाजको बनोट पनि टेस्ट ट्युब जस्तो टाइपको हुनु पर्यो किनकि अस्वाभिक रुपमा पानीको सतह पानीजहाजको सामान्य भन्दा माथिल्लो तह सम्म आउनु पर्ने हुन्छ र यो सम्भब छैन किनकि जहाजमा त झ्याल ढोका होलान चित्रको जस्तो गिलास बनोटको जहाज त कहिँ पनि छैन होला नि.या त त्यो भाईले गरेको जस्तै गरि गिलासमा जहाज हाल्नुपर्यो. संसारमा अहिले सम्म बनेको कुनै पनि पनि जहाजलाइ मात्रै ट्यांकरको पानीमा तैराउन जहाजको स्वभाबिक बनोटले सम्भब हुन दिदैन.
तपाइले भनेको कुनै कुरा बाझेको छैन, अवश्य पनि पहिलो गिलास गहिरो हुनुपर्छ ता कि पानी चुलिएर बाहिर नजाओस | र जहाजलाइ थोरै पानीमा पनि उतार्ने कुरामा “बढाई-चढाई” भनेको सत्य भए पनि प्राक्टिकल छैन भन्ने बुझिन्छ | यहाँ भन्न खोजेकै गिलासमा जस्तै गरि ठ्याकै जहाजको आकारको गहिरो भाँडोमा डुबाउने हो भने त्यस्तो हुन सक्छ भन्या हो |
ल साथिहरु आफु त हिसाव मा जिरो नै परियो !! के को पत्ता लगाउन सक्नु र गल्ति 🙁 तै पनि मिडिया मा त के जाति सम्पादक , प्रधान सम्पादक आदि पनि हुन्छन नि होइन र ? कुनै पनि समाचार दिनु अघि त्यसलाई पुष्टि गर्ने काम पनि त हुनु पर्यो नि, अरुको वारेमा भंगेराको टाउको जत्रो अक्षरमा व्यानर न्युज लेख्ने अनि गल्तिवस समाचार छापिएछ भनेर ११ पेजमा वर्गीकृत विज्ञापन दिने सम्पादक महोदय ले पत्रिकामा प्रकाशित हुने सम्पूर्ण जिम्मेवारी लिनु पर्ने होइन र अनि गलत समाचार लेखे वा प्रकाशित भए नैतिकताको आधारमा के के पो गर्नु पर्ने होइन र ? यो देशमा पत्रकारिता कि त ऋषि धमलाले पढेका छन् कि नेपालमा लोकतन्त्र ल्याउने पत्रिकाको मालिकले पढेका छन, वांकी त सव सिकारु नै हुन् नि . ल जा त भनिदिए मैले पनि उपबुज्रुक भएर
मित्र हो,
आदि इत्यादी कुराले गर्दा नै पत्रिका चलेका हुन्छन
थुप्रै बर्ष अगाडी मैले पनि एउटा यस्तै बैज्ञानिक भेट्टायको थिए!
पसलमा चन्दा माग्न आथ्यो उसले लेखेको बैज्ञानिक शिद्दान्तको एउटा किताबको ठेली लिएर, प्रकाशित गर्न चन्दा चाहियो भनेर!
प्रकाशको परावार्तक होकी आवर्तक केकेहो भन्थ्यो अहिले त बिर्सियो तेस्को फेद र टुप्पा, गुदी मात्र अलिअलि याद बाकि रहदा यो ब्लगको कुराले पुन झल्को दियो!
त्यो ठेली किताब पढ्ने त कुरा भयन तेसैले के हो भनेर सोध्दा यस्तै केकेहो प्रकाशले तय गर्ने यात्रा अनि बायु बिहिन खालि स्थानमा प्रकाश यात्रा गर्दैन केकेहो भन्थ्यो झोक चलेर झनक्क रिष उठ्याथ्यो, उसको त्यो सबै किताब त पढिएन र पढ्ने कुरानी भयन तर उसले जे भन्या थ्यो त्यो कुरालाई तेही उसकै अगाडि प्रयोगगरी गलत साबित गरिएयर पांच रुपैया (जे भयपनी उसले केहि दुख त गरेको थियो र माग्न आयको थियो चोर्न लुट्न होइन भनेर पांच रुपैया (आजको भ्यालुमा ५०० हुन्छ होला) दिएर,
” यस्ता नचाहिदो नचाहिदो सोध र खोज गर्नु भन्दा बरु खुरुक्क तरकारी उमार्नु धान फलाउनु, खेतिबाढि गर्नु नि!” भनेर पठायको थिए!
ति युवाले उनका विज्ञान का शिक्षक/गुरुलाई त देखाएकै हुनुपर्छ !
तेही भएर विज्ञान बा का यी शब्दहरु अति मनन गर्ने योग्य छन: ति युवा पूर्ण रुपमा गलत हैनन् — कुनै पनि कुरामा जिज्ञासा राखेर प्रस्न गर्नु नै अनुसन्धानको शुरुवात हो र बिज्ञानको बिकासको शुरुवात हो । यस्ता युवाहरुनै भोलि केहि गर्न सक्छन । तर हाम्रोमा खाँचो छ — राम्रो मेन्टरिंगको (या गाइडको) ।
“Little knowledge is dangerous knowledge”
एकदम राम्रो लेख बिज्ञान बा. सारै ज्ञान्बर्दक लाग्यो र एकदम चेतनामुलक छ…धन्यबाद.
नेपाल मा बिज्ञान सम्बन्धि येस्ता लेख आउन जरुरि छ…
I found exciting link below.
https://www.facebook.com/prcbk
कुनै स्थापित सिध्दान्तको विपक्षमा सोच्नै हुन्न भन्ने कुरा होइन तर त्यसको अपूर्णता दावी गर्दा कम्तिमा तत् सम्वन्धी विषयमा अनुसन्धानको अनुभव भएका बिशेषज्ञहरूसंग परामर्श लिन उत्तम हुन्छ ।
कुनै इलेक्ट्रोनिक्स सम्वन्धी म्यागाजिनमा भएका सर्किटको जडानलाइ कहिले काही अाविश्कारको रूपमा मेडियामा अाइदिन्छ, यो कुरा हाम्रो पत्रकारिता क्षेत्रमा उक्त विषयका दक्ष सन्चारकर्मीको अभावले हो । विज्ञानका मेधावी विद्यार्थीहरूले पार्टटाइम कामको रूपमा पत्रिकाहरूमा विशेष सम्वाददाताको रूपमा काम गर्दा पनि यो समश्याको हल हुन्छ ।
एउटा अर्को नि बिध्वान हुनुहुन्छ जसले आइन्स्टाइन,न्युतन हरुको फर्मुला गलत भनेर किताबनै छापेको छ , ३ बर्ष अगि भृकुतिमन्दप म भेतेको , मैले नि तपाइले माथी गरे को जस्तै १० क्लासमा पढ्दा बनाको फोर्मुला बात कुनै म १=२ , ३=७,13=25 almost (x+Y) or कुनै पनि २ वता नम्बर लाई बाराबर गरेर देखाए र उन्लाई सोधे आब तपाइ आफ्नो थ्योरी बुझाउनुस भनेको त सब के के हो ईन्टरनेट बात कपि गरेका कुरा हरु रेफ्रेन्श को रुप म देखयो जुन उ आफै पनि बुझ्दैन थ्यो । ।त्यो बूक अहिले नि बजार मा पाइन्छ नाम भने थाभ्एन । । ।एस्तै छ nepal ma
धेरै पहिले Einstain को Theory गलत साबित गरे भन्दै 10 क्लास को केटो सायद नासाको कुनै ठुलो सम्मेलनमा पुगेको थियो. समेलनमा खासमा उसले केहि नबुझेको ज्ञात भयो होला तेसपछि उसको News नै आएन. सायद उसले Newton को Motion सम्बन्धि ३ वटा नियम भन्दा पनि राम्रो अर्को नियम बनाएको भन्ने पनि कुरा गर्दै थियो.
कुनै Theory अरु भन्दा केहि फरक गर्छु भनेर बन्ने होइन स्मरण रहोस Special Theory of Relativity को लागि Einstain ले आफ्नो जीवनको ३६ वर्ष लगाएका थिए|
धेरै पहिले आउनु पर्ने News आज आयो खुसि लाग्यो.
नेपाल मा एस्त बकम फुसे हरु ले गलत्भंने र एस्त लै बुझ्दै नबुझी छाप्ने छापा हरु ले देश को बद्नाम पो गर्दिअछन र बकम्फुसे बैज्ञानिक निस्कनिदै अलाप हुँदै छन् धुपौरे हरु .
राम्रो लेख | शिर्षक “यसरी दिइन्छ यहाँ आइन्स्टाइनलाई चुनौति” को सट्टा “यसरी दिइन्छ यहाँ आर्किमिडिजलाई चुनौति” भएको भए अझ उत्तम हुन्थ्योकि जस्तो लाग्छ|
Oh forgot to mention, your square root step is wrong. When you take square root, you get both + and – results. You only considered +.
एक दम राम्रो लग्यो, बिज्ञान बा! You explained it so well.
बिज्ञान बा,
Simple but very nice explanation of the principle. Thanks a lot. Couple you please give us a link (or any info) of the article published in the national daily?
Thanks
The mistake is pretty obvious. Just because two squares (a square and b square) are equal does not mean a= b.
For example, 9 can be square of -3 or 9 can also be a square root of +3. So having squares of 9 does not mean -3=3
In the above example,
(4-9/2) ^2 = (-0.5)^2
(5-9/2)^2 = (+0.5)^2
Hence, eventhough square of -0.5 and +0.5 is same, but we cannot say -0.5=+0.5
साथी ले square root लाई तेसरी काट्न मिल्दैन तेसैले ४=५ हुदैन.
4 = 4
(2) squared = (-2) squared, but this does NOT mean 2 = -2 . The error is at the step you took the square root.
१००% agreed.
It is embarassing to read those news articles with claims of challenges to Einstein and Archimedes by नेपालक स्क्कुले युवा/ The reporters covering such news should atleast be qualified to understand what they are writing and if not atleast should seek a second opinion from a scientist in kirtipur before publishing such news articles.
It is one thing to publish artlcles about baseless Nepali politics and daily social matters. But it is embarrassing to refute laws of physics without even understanding it properly. नत्र अस्ति नै पढेको ब्याट्रीको कालो धुलो र कालिमाटीको कथा जस्तो हुन्छ बिज्ञान भनेको / नेपालमा चिया पसलमा बसेर गफ लगाउन मात्र ठिक्क
बर्ग मूल मा गल्ति / +- … = +- … ४ क्लास को हिसाब किताब बिस्तृत कुरो धमला लाइ सोध्नुस /
सुरुको गणित नबुझ्ने साथीभाईलाई :
Square-root लिदाको उत्तरमा + र – दुवै चिन्न लिनुपर्छ | माथि दुबैतिर + मात्र लिएकोले गलत भएको हो | सहि उत्तर
±(4 – 9/2) = ±(5 -9/2) हुन जान्छ |
जुन अरु हिसाब गर्दा,
-1/2 = -1/2 या 1/2 = 1/2 हुन जान्छ 4 = 5 हुदैन |
राम्रो छ तर + र – एक तिर मात्रै लिने हो. दुवै तिर लिनु को कुनै अर्थ हुदैन.
यसमा + र – गल्ति होइन / खासमा ति square root 2 बराबर होइन / यो २=२ काटेको गल्ति हो किनभने base equal छैन भने square root बराबर हुन्दैन / (4-9/2)(4-9/2)=(5-9/2)(5-9-2) यसमा काट्ने कुनै आधार नै छैन /